Table of Contents
The Scholar of Alexandria
Eratosthenes of Cyrene, born around 276 BCE, was a scholar whose expertise spanned multiple disciplines, making him one of the most accomplished intellectuals of his time. As the chief librarian of the Library of Alexandria, he had access to an unparalleled collection of knowledge, which fueled his innovations in mathematics, astronomy, and geography. His contributions included the first recorded attempt to establish a system of latitude and longitude, a crucial advancement for future cartography. However, his most extraordinary accomplishment was his calculation of Earth’s circumference, achieved without modern tools or long-distance travel. By relying on logical deduction and geometric principles, Eratosthenes demonstrated that complex scientific discoveries could emerge from simple observations, revolutionizing the study of geography.
At a time when empirical science was still developing, Eratosthenes’ work showcased the power of reasoning in understanding the natural world. He applied mathematics to practical measurement, proving that theoretical knowledge could yield groundbreaking discoveries. His method for calculating Earth’s size combined the use of shadows, angles, and proportional reasoning, a technique that would later influence scientific methodologies for centuries. His success proved that technological limitations did not hinder intellectual progress; instead, curiosity and innovation could overcome barriers. His work laid the foundation for future scholars and explorers, reinforcing the idea that knowledge grows through observation and deduction.
The Premise: Earth’s Sphericity
Before Eratosthenes made his groundbreaking calculation, the idea of a spherical Earth had already gained acceptance among ancient scholars. As early as the 6th century BCE, Pythagoras theorized that celestial bodies, including Earth, were round based on their observed motions. Aristotle later provided stronger evidence, noting that Earth cast a curved shadow on the Moon during a lunar eclipse, a phenomenon impossible on a flat surface. Additionally, travelers heading south reported seeing new constellations appear above the horizon while northern stars disappeared, further suggesting a curved Earth. Despite these compelling observations, no one had attempted to measure Earth’s actual size, leaving the question of its scale unanswered until Eratosthenes’ experiment.
Unlike earlier philosophers who relied on theoretical reasoning, Eratosthenes sought direct measurement, applying mathematical precision to solve a fundamental geographic question. His approach marked a shift from abstract speculation to empirical science, demonstrating that Earth’s vast dimensions could be determined through careful observation and logic. His experiment was a pioneering step in quantitative geography, using shadow angles and proportional calculations to derive numerical proof. By treating geography as a measurable science, he set the stage for future advancements in cartography and astronomy. His work proved that scientific understanding could move beyond philosophical debate, creating a foundation for generations of scholars to refine and expand upon.
Observations in Syene
Eratosthenes became fascinated by reports describing a unique solar event in Syene, a city in southern Egypt, where the Sun stood directly overhead at noon on the summer solstice. This meant that tall, vertical objects cast no shadows, and sunlight reached the bottom of deep wells without obstruction. Such an occurrence suggested that Syene was positioned in a precise location relative to the Sun, allowing its rays to strike the ground perpendicularly. This observation held significant implications for understanding Earth’s shape. If Earth were flat, this phenomenon would be seen simultaneously at all locations, but reports confirmed that in other cities, including Alexandria, shadows were still present at noon, hinting at a curved surface.
Realizing the importance of this contrast, Eratosthenes devised a way to use it for measurement. He reasoned that if the Sun’s rays were parallel when reaching Earth, then differences in shadow lengths between two cities must be caused by the planet’s curvature. If Syene experienced no shadow, while a city farther north did, the difference in the Sun’s angle could reveal Earth’s size. This was an extraordinary leap in scientific thinking, as it showed how simple observations could provide numerical proof of a concept previously understood only in theory. By methodically comparing shadow angles and distances between cities, Eratosthenes laid the foundation for his famous calculation, proving that large-scale measurements could be achieved using logic, geometry, and careful observation.
Shadows in Alexandria
Eratosthenes, having determined that the arc between Syene and Alexandria accounted for 1/50th of Earth’s total circumference, needed an accurate measurement of this segment. Fortunately, the distance between these cities was well-documented through Egyptian trade records, estimated at 5,000 stadia. The stadion, an ancient Greek unit of measurement, varied in length, but a common estimate places it at around 157.5 meters. Using this conversion, 5,000 stadia equaled approximately 787.5 kilometers. This key measurement allowed Eratosthenes to extrapolate Earth’s full circumference using proportional reasoning, transforming a local distance into a planetary-scale calculation with remarkable precision.
With this distance established, Eratosthenes multiplied 787.5 kilometers by 50, arriving at an estimated total circumference of 39,375 kilometers. This was remarkably close to modern measurements of 40,075 kilometers, with an error margin of less than 2%. His astonishing accuracy was achieved using only simple tools, observational skill, and geometric principles. His experiment proved that large-scale measurements could be accomplished through careful study and logical reasoning. His method became one of the earliest examples of applied mathematics in geography, laying the groundwork for future advancements in cartography, astronomy, and scientific measurement.
The Geometric Insight
Eratosthenes demonstrated extraordinary reasoning by recognizing that the angle he measured in Alexandria was a small fraction of Earth’s full circular shape. The 7.2-degree difference in shadow length was equivalent to 1/50th of a complete 360-degree circle, meaning the distance between Syene and Alexandria represented 1/50th of the planet’s total circumference. This insight required a fundamental understanding of geometry and proportional relationships. Eratosthenes also relied on the assumption that the Sun’s rays traveled in parallel lines when reaching Earth, which was reasonable given the Sun’s vast distance. By applying these principles, he took what appeared to be an astronomical mystery and converted it into a precise, measurable mathematical problem.
Eratosthenes’ method was a groundbreaking application of mathematics to physical science, demonstrating how logic and measurement could be used to determine enormous distances. His approach simplified the challenge of calculating Earth’s circumference, showing that a large-scale measurement could be obtained from two relatively close locations using simple tools. This was an early example of applied mathematics, where numerical principles were not just theoretical but could be used to derive real-world conclusions. His work laid the foundation for future advancements in geography and astronomy, proving that careful observation, combined with mathematical reasoning, could unlock some of the universe’s greatest secrets.
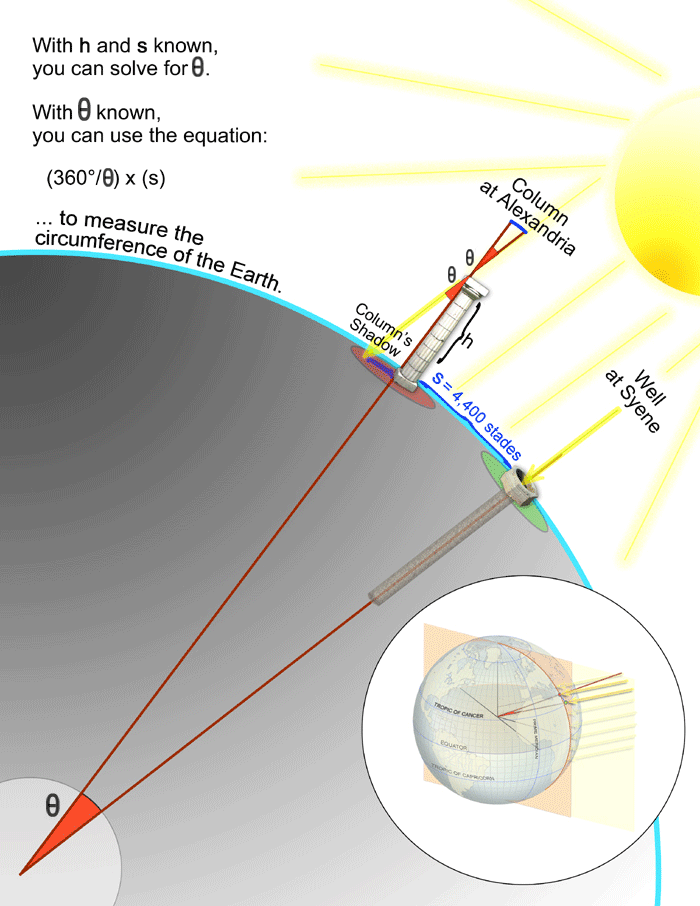
Measuring the Distance
Eratosthenes, having determined that the arc between Syene and Alexandria accounted for 1/50th of Earth’s total circumference, needed an accurate measurement of this segment to complete his calculation. Fortunately, the distance between these two cities was well-documented through Egyptian trade records and travel accounts, estimated at 5,000 stadia. The stadion, a unit of measurement used in ancient Greece, varied in length depending on the region, but a widely accepted value places it at around 157.5 meters per stadion. Using this conversion, 5,000 stadia equated to approximately 787.5 kilometers. This figure provided the essential data point Eratosthenes required to extrapolate the full circumference of the planet using proportional reasoning.
With this distance established, Eratosthenes multiplied 787.5 kilometers by 50, arriving at an estimated total circumference of approximately 39,375 kilometers. This result was remarkably close to modern calculations, which place Earth’s actual circumference at about 40,075 kilometers, showing an error margin of less than 2%. His astonishing accuracy was achieved without advanced measuring instruments or technology—just observational skill, logical deduction, and geometric principles. The precision of his work demonstrated the effectiveness of applied mathematics and scientific reasoning, proving that large-scale measurements could be accomplished with careful study and proportional calculations.
Calculating Earth’s Circumference
Eratosthenes’ method of determining Earth’s circumference was a groundbreaking achievement that demonstrated the power of mathematics and observation. By using simple tools, logical deduction, and geometric principles, he calculated the planet’s size with remarkable accuracy. His estimate, roughly 39,375 kilometers, was astonishingly close to modern satellite measurements, which place Earth’s circumference at about 40,075 kilometers. This level of precision, achieved over 2,000 years ago, was unprecedented, especially considering the limited technology of his time. His work proved that even vast distances could be measured with careful observation and mathematical reasoning. Eratosthenes’ experiment remains a prime example of how scientific discoveries can be made using ingenuity and logical thinking.
The impact of Eratosthenes’ findings extended far beyond his lifetime, shaping the future of geography, astronomy, and science. His work demonstrated that Earth could be studied through measurement and calculation, rather than speculation. Later scholars, including Claudius Ptolemy, used his methods as a foundation for further advancements in cartography and celestial studies. His experiment also influenced early explorers who sought to navigate the globe with greater precision. Even today, his approach is replicated in classrooms worldwide, allowing students to rediscover his method and appreciate its brilliance. His calculation was not just an intellectual triumph but a turning point in human understanding, bridging the gap between abstract thought and empirical science.
Assumptions and Accuracy
Eratosthenes’ groundbreaking experiment relied on several assumptions, each of which contributed to the accuracy of his final calculation. He assumed that Syene was precisely on the Tropic of Cancer, meaning the Sun would be directly overhead there at noon on the summer solstice. Additionally, he believed that Alexandria was located directly north of Syene along the same meridian, forming a perfect straight-line measurement. While these assumptions were not entirely correct—Syene is slightly off from the Tropic, and Alexandria is somewhat westward—the discrepancies were minor. Because the difference was small relative to the scale of the calculation, Eratosthenes’ final result remained impressively close to the actual circumference of the Earth.
Another key assumption was that Earth’s curvature was uniform, meaning it formed a perfect sphere. In reality, Earth is slightly oblate, bulging at the equator due to rotational forces. However, for the scale of measurement Eratosthenes was working with, treating Earth as a perfect sphere was a reasonable simplification. His reliance on the assumption that the Sun’s rays were parallel when reaching Earth was also valid, given the Sun’s immense distance from the planet. Despite minor inaccuracies, his logical approach and use of proportional reasoning ensured that his estimate remained within 2% of modern measurements. His method exemplified how scientific progress is built upon sound reasoning, even when minor approximations are necessary.
Legacy of the Experiment
Eratosthenes’ experiment was revolutionary, not only for its accuracy but for proving that scientific discovery could be achieved through observation and reasoning rather than advanced tools. His ability to measure Earth’s circumference using shadows, basic geometry, and logical thinking demonstrated that complex scientific problems could be solved with simple but effective methods. This approach laid the foundation for future scientific advancements, showing that understanding the natural world required careful questioning and precise measurement. His work provided an early example of applied mathematics in geography, influencing scholars for centuries. By proving that large-scale distances could be calculated mathematically, Eratosthenes set a precedent for using logic to solve problems beyond direct human perception.
The influence of Eratosthenes’ experiment extended far beyond his time, shaping the development of astronomy, cartography, and navigation. His method of measuring Earth’s size inspired later scientists such as Ptolemy, who expanded on geographic calculations, and Copernicus, who used similar principles in heliocentric theory. Even today, his experiment is replicated in classrooms worldwide, teaching students the power of observation and mathematical reasoning. His approach remains relevant in modern science, demonstrating that progress is built on curiosity, careful study, and logical thinking. By turning a simple observation into a groundbreaking discovery, he helped establish a scientific tradition that continues to guide researchers and explorers in their quest for knowledge.
Modern Replications
Eratosthenes’ experiment remains one of the most widely replicated scientific demonstrations in classrooms worldwide. Using little more than a vertical stick, a ruler, and basic geometry, students can measure the angle of a shadow at noon and compare their results with those from a different location. By applying the same proportional reasoning that Eratosthenes used over 2,000 years ago, they can calculate Earth’s circumference with surprising accuracy. This simple yet profound experiment continues to show how observation and logical deduction can unlock complex scientific truths. It also reinforces the importance of mathematics in real-world applications, demonstrating that fundamental principles remain relevant across centuries of scientific progress.
Beyond classroom experiments, Eratosthenes’ method has been adapted for modern scientific studies and public science initiatives. Amateur scientists and educators organize global projects where participants in different countries measure shadow angles simultaneously, mimicking the original experiment on an international scale. In some cases, these replications incorporate modern tools like satellite data and GPS to refine results and compare historical accuracy. His experiment’s continued relevance highlights the enduring power of critical thinking and scientific inquiry. By re-enacting his method, students and researchers alike gain a deeper appreciation for early scientific advancements, proving that knowledge built on observation and reasoning remains fundamental to understanding the world today.
The Power of Simple Observations
Eratosthenes’ experiment serves as a powerful reminder that groundbreaking discoveries often begin with simple observations. He did not have access to advanced instruments or extensive travel but relied on his ability to question the natural world. By noticing that shadows behaved differently in Syene and Alexandria at the same time of day, he uncovered a key piece of evidence about Earth’s shape and size. His method exemplifies how careful observation, combined with logical reasoning, can lead to profound scientific conclusions. Many great discoveries, from Newton’s theory of gravity inspired by a falling apple to Galileo’s observations of planetary motion, follow this same principle—where curiosity sparks revolutionary insights.
The importance of Eratosthenes’ work extends beyond measuring Earth’s circumference; it highlights the role of empirical evidence in science. His findings were based on measurable, repeatable observations rather than abstract speculation. This approach laid the foundation for the scientific method, which relies on testing and verifying ideas through direct evidence. His success demonstrated that even with limited resources, knowledge could be expanded through systematic inquiry. Today, his experiment continues to inspire scientists and students alike, showing that the most fundamental questions about the universe can often be answered by simply paying close attention to the world around us.
Inspiring Future Generations
Eratosthenes’ groundbreaking work continues to inspire scientists, mathematicians, and educators, demonstrating the power of curiosity and logical reasoning. His ability to measure the vast circumference of the Earth with only basic tools highlights how innovation arises from critical thinking rather than advanced technology. His legacy encourages students to question the world around them, just as he questioned why shadows differed between cities. Many modern scientific fields, including astronomy, physics, and geography, build upon the same principles of observation and deduction that he used. By showing that even large-scale problems can be solved through logic and simple mathematics, Eratosthenes remains a role model for those who seek to understand and explore the natural world.
The scientific method thrives on building knowledge from past discoveries, and Eratosthenes’ work exemplifies this principle. His experiment demonstrated that human understanding is a cumulative process, where each generation refines and expands upon previous knowledge. Today, his method is taught in classrooms as an example of how science progresses through inquiry and systematic measurement. His legacy reminds us that major advancements often begin with a single observation and a willingness to challenge conventional thinking. By continuing to encourage curiosity and problem-solving, his story serves as a testament to the enduring value of scientific exploration and the limitless potential of the human mind.
